Pole koła, pole trójkąta Nicky: Na trójkącie ABC, w którym IACI=IBCI, opisano okrąg o środku O i promieniu R=20cm. Wiedząc, że kąt AOB=120⁰, oblicz pole trójkąta ABC oraz długość promienia okręgu wpisanego w ten trójkąt. Rozważ dwa przypadki. W odpowiedziach pisze, że trzeba odnieść się do trójkąta równobocznego i rozwartokątnego. Z równobocznym nie miałam problemu, ale z tym drugim tak. Pomoże ktoś?

ICSP: Masz do tego odpowiedzi?

Potrzebująca: Odnośnie rozwartokątnego P=100√3cm², r=(20√3−30)cm

ICSP: ooo Dobrze mi wyszło xD

Potrzebująca: A wytłumaczysz mi to?

ICSP: Rozwiazanie wrzucę później. Teraz niestety muszę wychodzić. Jak chcesz mozesz sama pokombinować. Tam romb powstanie. Wzór na pole rombu: P = a²sinα.

	1
a wzór na Pole tójkąta to : P =		absinα i właśnie z tego wzoru powinnaś wyliczyć sinusy z
	2

tamtego zadania

Potrzebująca: Ok, może jakoś sobie poradzę, ale i tak dziękuję za pomoc

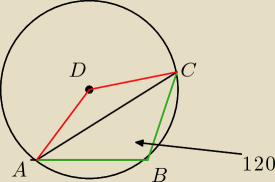
ICSP: czerwone odcinki to promienie. Zielone docinki to dwa boki trójkąta. Czworokąt ABCD jest rombem dlatego zielony = czerwonemu = 20

	1
kąt DAB = 60o czyli pole ΔABC =		PrombuABCD
	2

	√3
PrombuABCD = sin60o * 202 = 400*		⇔ PΔABC = 100√3
	2

|AC| = 20√3

	20 + 20 + 20√3
P =		*r
	2

200√3 = (40 + 20√3)r

	10√3
r =		= 10√3(2−√3)
	2 + √3

Koniec.

Potrzebująca: Super! Dzięki Teraz sobie to przeanalizuje i jak będę miała pytania, to napiszę =]

Potrzebująca: A z jakiego wzoru skorzystałeś, by obliczyć r?

Potrzebująca: Dobra, wiem już =]